Problemas: ley de los senos y cosenos

4.  Un faro F puede ser visto desde dos puntos, A y B. La distancia AB es de 748 m; el ángulo FAB mide 68°47´ y el ángulo FBA mide 79°28´. Calcúlese la distancia AF.

Realicé un dibujo rápido y queda así: 

De acuerdo a la ley de los senos: tenemos que AB/(sin(∠F)=AF/(sin(∠B), simplemente despejamos AF, lo que nos queda como AF=AB*sin(∠B)/(sin(∠F), y aquí simplemente sustituimos y resolvemos, AF=748*sin(79°28´)/sin(180-79°28´-68°47´)=748*sin(79°28´)/sin(31°45´), lo que es semejante a 1397.521.

5.  Una diagonal de un paralelogramo mide 34.28 dm y forma ángulos de 22°27´ y 46°14´ con los lados. Calcúlese la longitud de cada lado y la superficie.

Bueno, para empezar, esta claro que un paralelogramo que se divide entre 2 por la diagonal, tiene un ángulo obtuso y 2 agudos, lo primero que haremos será utilizar nuevamente la ley de los senos AB/sin(∠C)=AC/sin(∠B), en este caso seria, BD/sin(∠C)=DC/sin(∠B)=CB/sin(∠D), y si despejamos obtendremos, DC=BD*sin(∠B)/sin(∠C)=34.28*sin(46°14´)/sin(180°-46°14´-22°27´)=34.28*sin(46°14´)/sin(111°19´), lo que nos da un aproximado de 26.5737 dm; CB=BD*sin(∠D)/sin(∠C)=34.28*sin(22°27´)/sin(111°19´) lo que se asemeja a 14.0521 dm, y con esto ya tenemos los valores de los lados: 26.5737 dm y 14.0521 dm respectivamente, y para sacar la superficie, es decir el área, por comodidad sacaré el área de un triángulo y lo multiplicaré por 2, y para sacar el área del triángulo simplemente utilizaré la formula de Heron, lo que nos dejaría con S(ABC)=√s*(s-a)*(s-b)*(s-c), s es el semiperímetro, es decir, la mitad del perímetro, por lo tanto s=(26.5737+14.0521+34.28)/2, una vez aclarado esto, sigamos, √(37.4529)*(37.4529-34.28)*(37.4529-26.5737)*(37.4529-14.0521)=√30253.07341706; y esto se asemeja a 173.9352 dm, esto simplemente se multiplica por 2, lo que nos da un área de 347.8704 dm^2.
Dato curioso, me gusta hacerlo lo más perfecto posible, y para sacar el área realicé esto

 casi no se ven los valores*

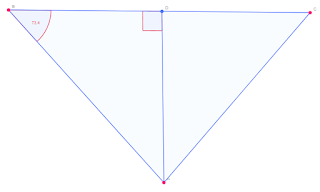
6.  Los lados paralelos de un trapecio miden 27 dm y 14 dm, y los ángulos que forma la base mayor con los lados no paralelos, son de 59°28´ y 73°24´. Calcúlese la longitud de los lados no paralelos y la superficie del trapecio.

Lo primero que realizaremos será juntar las 2 partes externas (los 2 triangulitos) en uno solo, en el cual podamos trabajar con más facilidad.

Una vez ya tenemos esto, es fácil notar que ya poseemos 2 ángulos y la base, que equivale a la diferencia entre las bases (27-14=13), y ya con esto, lo que buscaremos obtener serán los otros 2 lados del triángulo, y simplemente utilizar la ley del seno BC/sin(∠A)=AB/sin(∠C)=AC/sin(∠B), es decir, 13/sin(180-59°28´-73°24´)=13/sin(180-132°52´)=13/sin(47°8´)=AB/sin(59°28´)=AC/sin(73°24´), AB=13*sin(59°28´)/sin(47°8´)=15.2773; AC=13*sin(73°24´)/sin(47°8´)=16.9975, y ya con esto podemos obtener fácilmente la altura y con ello el área, la altura se puede obtener de la siguiente manera AB/sin(90)=AD/sin(73°24´), por lo tanto, AD=16.9975*sin(73°24´)*sin(90), esto nos da un aproximado de 14.65918283, ahora con esto ya podemos obtener el área, simplemente con lo siguiente, Área=(b+B)h/2=(14+27)14.65918283/2, lo que nos daría un área aproximado de 300.51324817

7.  Dos colinas, de forma cónica, se tocan por sus bases, que se hallan en el mismo plano horizontal, y sus laderas, consideradas en el mismo plano vertical, forman un ángulo de 72°. Una de las laderas mide 410 m y forma con la visual a la otra cima un ángulo de 57°24´. ¿Qué distancia hay entre las cimas de las colimas?

Así queda la figura, realmente, una vez ya tenemos estos valores, es fácil obtener el otro ángulo, el opuesto al lado del cual tenemos el valor, y ya con esto, gracias a la ley del seno AB/sin(∠C)=BC/sin(∠A), es decir, AB=BC*sin(∠C)/sin(∠A); es decir, AB=410*sin(72)/sin(180-72-57°24´)=410*sin(72)/sin(50°36´), lo que se asemeja a 504.6152 metros, lo que seria la respuesta.

8. Dos vías férreas, que parten de una misma estación, forman entre sí un ángulo de 37°28´. Dos trenes parten al mismo tiempo. La velocidad de uno es de 54 km/h y la del otro es de 60 km/h. ¿A qué distancia estará uno del otro después de 25 minutos?

Esta claro que después de 25 minutos el tren A (cuya velocidad es de 54 km/h), ha viajado 22.5km, esto lo sabemos ya que es fácil notar que 54 km/h=(9/10) km/m, y con esto obtenemos que en 25 minutos el tren A ha recorrido 25*(9/10) km=9*2.5=22.5km, y para el otro tren tenemos algo similar, 60 km/h= 1 km/m, por lo tanto hemos recorrido 25 km, y ya con estos valores, es fácil ver con la ley del coseno (BC^2=AC^2+AB^2-2*AC*AB*cos(BAC)), y aquí simplemente queda sustituir los valores, lo que nos quedaría BC^2=25^2+22.5^2-2*25*22.5*cos(37°28´)=25^2+22.5^2-1125*cos(37°28´) =625+506.25-1125cos(37°28´)=1131.25+1125cos(37°28´), lo que se asemeja a 15.4379 kilómetros.

9. Dos observadores, A y B, situados en las orillas opuestas de un río, miden los ángulos de elevación del punto más alto del mástil de un barco, anclado en dicho río. Si la distancia AB es de 304 m, y los ángulos miden, respectivamente, 14°20´ y 8°10´, ¿Qué altura tiene el mástil? (Los observadores y el mástil están en un mismo plano vertical).

Para este problema lo primero que haré será conocer el valor del ángulo faltante, que en este caso seria el ángulo ACB, el cuál fácilmente podremos notar que equivale a 180°-14°20´-8°10´=157°30´, y con esto, gracias a la ley del seno podremos obtener la medida de uno de los lados faltantes, por ejemplo AC, tenemos que 304/sin(157°30´)=AC/sin(8°10´), por lo tanto AC=304sin(8°10´)/sin(157°30´), lo que es aproximadamente 455.61261284, y ya con esto, facilmente podremos obtener la medida de CD, nuevamente con la ley del seno, pues 455.61261284/sin(90)=CD/sin(14°20´), es decir, CD=455.61261284sin(14°20´)/sin(90), lo que nos da un aproximado de 446.87441603 metros.

10. Un puente horizontal de 23.8 m de largo, une 2 colinas cuyas laderas forman con el horizonte ángulos de 23° y 32°. ¿Cuál es la altura del puente con respecto al vértice del ángulo formado por las dos laderas?

Bueno... mi dibujo quedo así, y es fácil notar que los ángulos internos que se encuentran en la base larga del trapecio es lo mismo que los ángulos que nos dieron, y con esto, después de trazar las alturas es fácil trazar un triángulo que junte los triangulitos del trapecio en un solo triángulo, lo que nos queda:

Y con esto podemos obtener los ángulos internos del triángulo, cabe notar que la base del triángulo equivale

11. Dos barcos salen de un puerto al mismo tiempo. Uno navega hacia el sur con una velocidad de 34km/h, y el otro hacia el sur-sureste y su velocidad es de 25 km/h. ¡A qué distancia se hallarán después de media hora de marcha?

.

Esta claro que el ángulo formado entre el sur y el sureste es de 45°, luego, es fácil notar que después de 1/2 hora de recorrido, habrán recorrido la mitad de lo que hacen en 1 hora, por lo tanto el tren S esta a 17 km del punto de origen, y el tren B esta a 12.5 km del punto de origen, luego el fácil utilizar la ley del coseno para obtener el valor deseado (BS^2=AS^2+AB^2-2*AS*AB*cos(BAS)), aquí sustituimos los valores, y nos queda BS^2=17^2+12.5^2-2*17*12.5*cos(45)=17^2+12.5^2-2*17*12.5*(√2)*/2=289+156.25-(√2)*212.5=445.25-(√2)*212.5, y después nos queda sacar la raíz cuadrada de esto, lo que se asemeja 12.03036 km.